PECAHAN

MAKSUD : Nombor yang mewakili sebahagian daripada keseluruhan atau sekumpulan benda.
Mengikut sejarah, "pecahan" merujuk kepada sebarang nombor yang tidak mewakili keseluruhan.
Nombor yang kini dipanggil "perpuluhan", asalnya dikenali sebagai "pecahan perpuluhan"
Nombor yang kini dipanggil "pecahan", asalnya dikenali sebagai "pecahan kasar".
"kasar" (vulgar) bermaksud "biasa" (commonplace).
Digunakan apabila penyebutnya kecil.
Pecahan biasa atau kasar biasanya ditulis dalam satu pasangan nombor, nombor di atas dikenali sebagai pengangka sementara yang di bawah dikenali sebagai penyebut.

BENTUK PECAHAN

(a) (i)Pecahan Biasa

Pecahan kasar (atau pecahan biasa) ialah satu nombor nisbah yang ditulis dengan satu integer (pengangka) yang dibahagikan dengan satu integer bukan sifar (penyebut)

(ii) Pecahan Wajar

Pecahan kasar akan menjadi pecahan wajar apabila nilai mutlak pengangka adalah kurang dari nilai mutlak penyebut; yang menjadikan nilai mutlak keseluruhan pecahan kurang daripada 1.

(iii) Pecahan Tak Wajar

Pecahan kasar akan menjadi pecahan tak wajar apabila nilai mutlak pengangka adalah lebih besar atau sama dengan nilai mutlak penyebut (Contoh: 8⁄5)

(b) Nombor Bercampur

Campuran nombor bulat dan pecahan wajar.
Penambahan ini dinyatakan tanpa menggunakan tanda operasi seperti "+".
Contoh:
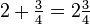
Satu pecahan tak wajar boleh digunakan untuk menyatakan satu nombor bercampur.
Contoh: 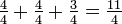boleh ditulis sebagai .

(i) Nombor bercampur boleh ditukar menjadi pecahan tak wajar dalam tiga langkah:

Darabkan nombor bulat dengan penyebut pecahan.
Tambah pengangka pecahan pada hasil darab di atas.
Hasil tambah langkah 2 adalah pengangka untuk pecahan (tak wajar) baru, dengan penyebut 'baru' nya kekal sama dengan penyebut untuk pecahan asal nombor bercampur.

(ii) Pecahan tak wajar juga boleh ditukar menjadi nombor bercampur:

Bahagikan pengangka dengan penyebut.
Hasil bahagi (tanpa baki) menjadi nombor bulat manakala bakinya menjadi pengangka untuk pecahan.
Penyebut baru untuk pecahannya adalah sama dengan pecahan tak wajar yang asal.

(c) Pecahan Setara

Dengan mendarab pengangka dan penyebut sesuatu pecahan dengan nombor yang sama (bukan sifar), hasil pecahan yang baru adalah setara dengan pecahan asal.
Perkataan setara bermaksud kedua-dua pecahan memiliki nilai yang sama yang mengekalkan integriti yang sama - Perimbangan dan perkadaran yang sama.
Contohnya, untuk pecahan : apabila kedua-dua pengangka dan penyebut didarab dengan 2, hasilnya adalah , yang memiliki nilai yang sama (0.5) dengan .
Membahagikan pengangka dan penyebut dengan nombor (bukan sifar) yang sama juga menghasilkan pecahan setara.
Ia dikenali sebagai mengurangkan atau memudahkan pecahan.
Satu pecahan yang pengangka dan penyebutnya tidak mempunyai faktor yang sama (selain 1) dianggap tidak boleh dimudahkan dan berada dalam bentuk termudah atau sebutan terendah.
Contoh $\tfrac{3}{9}$ bukanlah satu pecahan termudah kerana 3 dan 9 mempunyai faktor yang sama iaitu 3. Sebaliknya, $\tfrac{3}{8}$ ialah pecahan termudah kerana satu-satunya faktor untuk 3 dan 8 ialah 1.

(d) Salingan dan "Penyebut Halimunan"

Salingan sesuatu pecahan ialah pecahan dengan pengangka dan penyebutnya diterbalikkan.
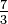Contohnya, salingan untuk $\tfrac{3}{7}$ , ialah $\tfrac{7}{3}$ .
Oleh kerana hasil bahagi sebarang nombor dengan 1 adalah sama dengan nombor itu, nombor bulat juga boleh ditulis dalam pecahan dengan menggunakan 1 sebagai penyebut: 17 = $\tfrac{17}{1}$ (kadang-kadang 1 dirujuk sebagai "penyebut halimunan").
Kecuali untuk sifar, setiap pecahan atau nombor bulat memiliki satu salingan.
Salingan untuk 17 ialah $\tfrac{1}{17}$ .

(e) Pecahan Kompleks

Pecahan kompleks (atau pecahan majmuk) ialah pecahan yang pengangka atau penyebutnya mengandungi pecahan.
Contohnya, 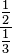$\cfrac{\tfrac{1}{2}}{\tfrac{1}{3}}$ dan $\frac{12\frac{3}{4}}{26}$ merupakan pecahan kompleks.
Untuk memudahkan satu pecahan kompleks, bahagikan pengangka dengan penyebut seperti dalam pecahan yang lain.

$\cfrac{\tfrac{1}{2}}{\tfrac{1}{3}}=\tfrac{1}{2}\times\tfrac{3}{1}=\tfrac{3}{2}=1\frac{1}{2}.$
$\cfrac{\tfrac{3}{2}}5=\tfrac{3}{2}\times\tfrac{1}{5}=\tfrac{3}{10}.$
$\cfrac{8}{\tfrac{1}{3}}=8\times\tfrac{3}{1}=24.$

MENUKAR PECAHAN KEPADA PERATUSAN

Untuk menukar pecahan kepada peratusan, pecahan tersebut perlu didarabkan dengan seratus peratus.
Contoh: 1/4 x 100% = 25%

MENUKAR PECAHAN KEPADA PERPULUHAN